Isla o copo de nieve de Koch

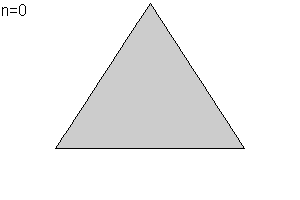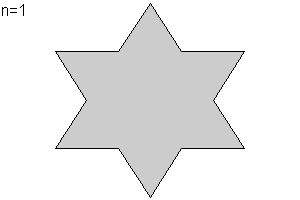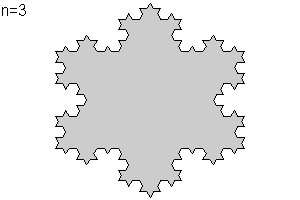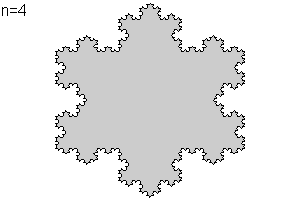
Se parte de un triángulo equilátero de lado unidad. Cada uno de los lados se divide en tres partes iguales de longitud 1/3. Se sustituye el segmento central por dos segmentos de tamaño idéntico formando un diente, tal como muestra la animación en la iteración n=1, y se obtiene una curva poligonal P1 de longitud = 3·4·1/3= 4.

Si se repite la operación, como se muestra en la animación en las iteraciónes: 2 (n=2), 3(n=3), 4(n=4)..... ,la longitud de esta curva con un aumento de cuatro nuevos los "lados", por cada lado en cada iteración, evoluciona de acuerdo a la siguiente sucesión: 16/3, 64/9, 256/27 ,.... Dado que la sucesión anteriormente indicada no converge hacia ningún valor, estamos ante una curva de longitud infinita.

La iteración indefinida nos proporciona la isla de Koch o copo de nieve de Koch