|
| |
|
Cualquiera que sea el método de aproximación al concepto de fractal que
utilicemos hay un concepto central que es el de dimensión, quizás por ello,
el concepto de dimensión fractal esta esparcido por la literatura científica
y se utiliza muchas veces indiscriminadamente creando confusión.
Aquí analizaremos la dimensión fractal abordando previamente el concepto de
dimensión topológica para ser consecuentes con la propia
definición de Benoit B. Mandelbrot , de la que se deduce que
la dimensión fractal es mayor que su dimensión topológica.
Dimensión topológica, es un término que introdujo
Henri Poincaré (1854-1912), físico
francés y uno de los principales matemáticos del siglo XIX.
| |
|
|
Dimensión topológica |
|
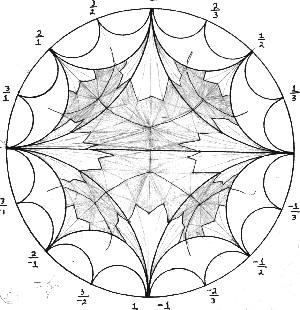
Representación sección Poincaré |
La dimensión topológica es fácil de comprender ya que nos habla de la
conectividad de los puntos del objeto de medida. En los
Elementos de Euclides, ya se define, implícitamente y de forma
inductiva, el concepto de
dimensión topológica euclidiana. Se
dice que una figura es unidimensional, si su frontera está compuesta de
puntos; bidimensional, si su frontera está compuesta de curvas y
tridimensional, si su frontera está compuesta de superficies.
Profundizando un poco más y desde
un punto de vista topológico sabemos que la circunferencia y
un segmento rectilíneo son la misma curva y encierran el mismo tipo de
superficie (pues es posible transformar una en la otra mediante una
deformación continua, ahora bien, desde un punto de vista métrico no son la
misma curva, ya que la circunferencia y el área que encierra, el círculo,
son finitos, y, en cambio, el segmento, aunque es finito, no encierra con su
borde un área finita. Aparece aquí, entonces, una característica moderna de
las matemáticas: intentar clasificar los objetos por lo que se conserva, por
los invariantes, y analizar, por otra parte, qué ocurre con lo que no se
conserva, cómo hay que analizarlo, qué hay que hacer con ello, cómo
integrarlo en el mundo de los entes matemáticos. En el ejemplo anterior, lo
que se conserva es su carácter topológico, es decir, su dimensión
topológica.
|
|
Señalaremos finalmente que el propio concepto dimensión tiene un significado
matemático muy amplio, y por lo tanto se ofrecen un amplio repertorio de
definiciones. Entre ellas existe siempre la
noción de recubrimiento del objeto
estudiado, por otra forma matemática cuyo diámetro tiende a cero.
Si tenemos en cuenta la definición inductiva de dimensión topológica dada
por Poincaré (" un objeto tiene dimensión topológica "m" cuando
cualquier recubrimiento de ese objeto, tiene dimensión topológica "m"), debemos añadir que el conjunto vacío tiene
dimensión –1.
Una definición distinta de dimensión
topológica es la definición por semejanza, llamada también de autosemejanza,
que sugirió Felix Hausdorff en 1919, readaptada posteriormente por
Besicovich (dimensión de Hausdorff-Besicovich) y que se
recoge en la definición de fractal que propone Benoit B. Mandelbrot.
|
| |
|
|
Dimensión fractal
|
|
|
1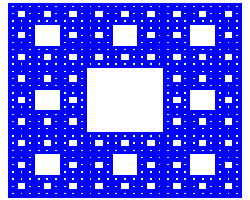
2

1. Alfombra de Sierpinski. 2. Esponja de Menger |
El concepto de dimensión en los fractales como consecuencia de la
recursividad o autosimilitud a cualquier escala que poseen es
algo muy complejo. Los
fractales están compuestos por elementos cada vez más pequeños de sí mismos
que se replican indefinidamente a menor escala,
generándose una figura que tiene una superficie finita con un perímetro de
longitud infinita y con un número infinito de vértices. En el lenguaje
matemático del cálculo, diríamos que esta curva no se puede diferenciar.
Por ello, el
concepto de dimensión juega un
papel fundamental en la geometría fractal. Pero el
dimensión en la mayoría de los fractales no
se ajusta a los conceptos tradicionales de la
dimensión euclidiana o dimensión topológica.
Más aún, su valor raramente puede ser expresado con un número entero.
La dimensión fractal, se puede definir de diferentes maneras, siendo la más
rigurosa la de Hausdorf y la más intuitiva y más fácil de aplicar es la de
semejanza. Antes de definirla se debe señalar dos aspectos importantes
relativos a la escala de medición y su relación con la expresión del tamaño
y con la dimensión topológica para destacar que:
La dimensión definida por Felix Hausdorff en
1919, y perfeccionada más tarde por Besicovitch esta recogida en la
definición de fractal que propone Benoit B. Mandelbrot :“Un fractal es,
por definición, un conjunto cuya dimensión de Hausdorff-Besicovitch es
estrictamente mayor que su dimensión topológica”.
|
|
De una forma intuitiva la dimensión Hausdorff H(X) de
un objeto fractal
X mide el número de conjuntos de longitud L que hacen falta para
cubrir X por L. Esta dimensión se representa por la siguiente fórmula:
S = LD
Donde S
es el tamaño del fractal, L la escala de medición D es la
dimensión fractal que buscamos. Operamos para despejar D:
log S = D log L
-------> D = log S / log L
Como veremos la dimensión de homotecia Hausdorff- Besicovitch,
es una generalización de la dimensión euclidiana, que con carácter general,
tiene valores enteros e iguales a la dimensión topológica para las líneas,
polígonos y sólidos y valores fraccionarios y superiores a su
dimensión topológica en los fractales.
Analizaremos algunos ejemplos de:
|

Curva de Peano
|
|
|